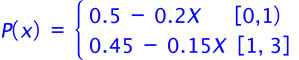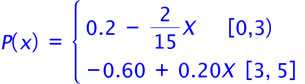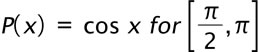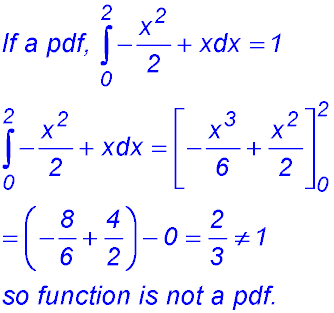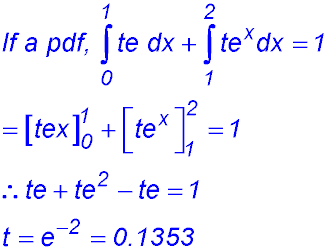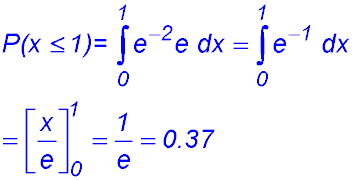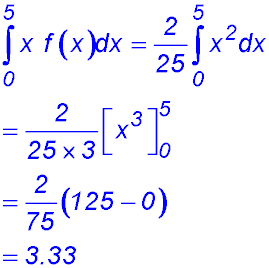Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Continuous probability density functions.
Test Yourself 1 - Solutions.


 

Properties.

1. (i) Gradient = -0.4÷ 5 = -0.08.

Intercept is pr = 0.4

∴PDF is P(X) = 0.4 - 0.8X [0, 5]

(ii) Area under the line:
0.5 × 0.4 × 5 = 1.0

∴ a pdf.
 

2. (i) Part 1:

Gradient = 0.2 ÷ (-1) = -0.2

Intercept is 0.5

∴ Eqn is P(X) = 0.5 - 0.2 X [0, 1]

Part 2:

Gradient = 0.3 ÷ (-2) = -0.15

P(X) = a - 0.15X

Passes through (3, 0)

∴ 0 = a - 0.15 × 3 ∴ a = 0.45

PDF is

(ii) Area 1: = 0.5×1× (0.5+0.3) = 0.4

Area 2: = 0.5 × 2 × 0.3 = 0.3

Total area = 0.7 - so NOT a probability density function.
 

3. (i) Part 1:

Gradient = 0.4 ÷ (-3)

Intercept is 0.4

∴ Eqn is

Part 2:

Gradient = 0.4 ÷ (2) = 0.20

P(X) = a + 0.2X

Passes through (3, 0)

∴ 0 = a + 0.2 × 3 ∴ a = -0.60

Eqn is P(X) = -0.6 + 0.2X

PDF is

(ii) Area 1: 0.5 × 3 × 0.4 = 0.6

Area 2: 0.5 × 2 × 0.4 = 0.4

Total area = 1.0 ∴ a pdf.
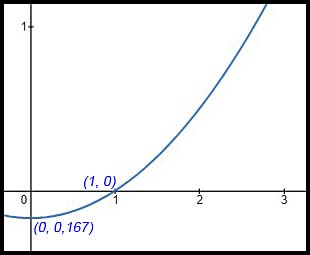
Probability density function. 4. Analysing the function

shows that:

  • all values of P(x) are negative (in the second quadrant of ASTC); and
  • the value of the definite integral is -1
    (think of the cos graph).

Hence P(x) satisfies neither of the properties of a probability density function.
  5. (i) .

(ii)

(iii) Although the definite integral for the given domain [0, 3] is 1.0, the y = f(x) values are negative for [0, 1] and it is not possible to have negative probabilities. Hence the function cannot be a probability density function.
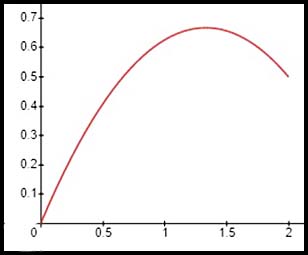
  6.
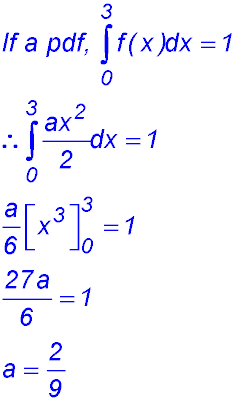  7. (i)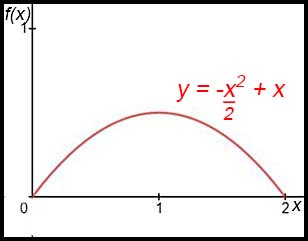

At x = 2, f(2) = 0

(ii)

(iii)

(iv)

Pr (x = 2) = 0.5.

 

8. (i)

(ii)

Comment: Click here.

(iii)

  9.
Uniformly distributed functions. 10. (i) ISS

 

 
   
Determining probability.  
Expected value and variance. 14.
  15. (i)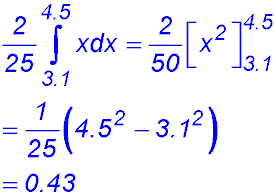

(ii)

(iii)

Find the mode.